Games Built the Computer: Babbage, Lovelace and the Dawn of the Ludic Age
by Samuel PizeloAbstract
This article argues that games were used as modeling technologies for the earliest symbolic computational device, the Analytical Engine of Charles Babbage and Ada Lovelace. Consequently, it is argued that the history of computing technology is one part of a longer history of games as modeling technologies. Before Babbage first wrote on the theory of computation in the 1820s, he had spent nearly a decade developing a “geometry of situation” through the study of games of skill, inspired by the work of German polymath Gottfried Wilhelm Leibniz. Babbage employed this new geometry to describe the operations of mechanical computers in space and over time in symbolic language. I argue that Babbage’s earlier study of games provided crucial tools and concepts for his later project of making a symbolic computational device. I also examine the discussion of games in Babbage and Lovelace’s earliest correspondence to argue that games continued to model crucial innovations in their design of the Analytical Engine. Examples of this include the use of punch card programs and the development of an “anticipating carry” to speed up computation. I demonstrate how Babbage and Lovelace relied on historically specific forms of games such as chess, solitaire and tic-tac-toe to develop a symbolic language describing the relationship between space, time and mechanism. This elemental correspondence between game form and computational architecture can provide computer game scholars with new ways of describing the relationship between computers and games. Recognizing the historical role of games as models foregrounds their ongoing epistemological influence.
Keywords: game history, models, algorithms, history of computing, Ludic Age, temporality, spatiality, game theory, mathematics, Charles Babbage, Ada Lovelace, Gottfried Wilhelm Leibniz
Introduction
Ada Lovelace prophesized the dawn of the information age in 1843, with her published translation of the “Sketch of the Analytical Engine invented by Charles Babbage.” Lovelace’s lengthy notes on the translation displayed an intimate familiarity with the proposed Engine, including a lucid speculation on the capacities of symbolic computation in the arts and sciences and a demonstration of a written program for computing the Bernoulli Numbers -- earning her the moniker of the “first programmer” (Toole, 1998). The Analytical Engine was qualitatively different from any prior computational device, such as Babbage’s 1822 Difference Engine, because it did not merely execute a particular form of linear operation -- the calculation of the differences between sequences of numbers -- but was “an embodying of the science of operations” itself through its ability to interpret symbolic operations (Lovelace, 1843, p. 161, emphasis in original). Electronic computers characterized the so-called technosciences by the end of the Second World War, but Babbage’s and Lovelace’s vision for symbolic computation would not be actualized until the late 1940s -- more than a century after Lovelace’s notes. Almost two centuries later, we are living the reality of this early vision.
What made the symbolic revolution possible? Babbage’s earlier research provides clues: in the winter of 1822, mere months after completing work on his first Difference Engine, he penned two texts expressing the desire for a more expansive device that was able to follow multiple sequential instructions. What usually escapes mention in histories of computation is that, in both texts, Babbage explicitly credits his realization of a need for this general calculating engine to his earlier mathematical analysis of games. In fact, a survey of Babbage’s early work on games provides ample evidence that the “science of operations” described by Lovelace was developed through an intimate study of the algorithmic logics of games. The symbolic revolution was first a ludic revolution.
In what follows, I will look to Babbage’s early publications, manuscripts, and notes as well as his earliest correspondence with Lovelace to trace a history of symbolic computation that began as the study of games. I will argue that Babbage and Lovelace used games as models of algorithmic operations, spatialized computation and predictive reasoning. These three aspects of games later became the three greatest innovations of the Analytical Engine: the science of operations, the spatial mapping of computation through punched card programming and the predictive mechanism of the “anticipating carry.” I follow a growing cadre of scholars who attend to the use of games as models and the epistemological consequences of these ludic practices [1]. By revisiting this early moment in the history of computation, I hope to provide insight into the historical consequences of game modeling as a means of describing the relationship between space, time and action. As scholars like McKenzie Wark, Alexander Galloway and Eric Zimmerman argue, game logics structure every aspect of life under late capitalism (Wark, 2007; Galloway, 2006; Zimmerman, 2015). Thus, a history of the diffusion of game logics is also a history of the present.
A New Science of Algorithms
Babbage first recognized the need for a new engine when he confronted a problem that his first engine could not solve. Completed in June of 1822, Babbage’s Difference Engine was designed to calculate tables of logarithms for navigation and astronomy -- a tedious and expensive task that previously required roomfuls of trained workers. Later that year, Babbage reflected on his achievement, noting that he had stumbled upon an entirely new “species” of mathematical problem that could only be solved algorithmically because its “analytical laws are unknown” (Babbage, 2010, p. 216). It was not the Difference Engine itself that inspired this new species of mathematics, however, but his study of the game of chess. He makes this connection explicit:
That the mere consideration of a mechanical engine should have suggested these inquiries, is of itself sufficiently remarkable; but it is still more singular, that amongst researches of so very abstract a nature, […] I should have met with and overcome a difficulty […] in attempting the solution of a problem connected with the game of chess. (Babbage, 2010, p. 222)
Babbage constructed several examples of this new species of problem in order to illustrate a single principle: most empirical sequences of numbers do not change uniformly and predictably. Instead, these sequences folded back on themselves and exhibited conditional logics -- for instance, calculate the exponents of 3 but increase the number by ten every time there is a “2” in the tens place [2]. This essentially algorithmic approach to mathematics was wholly foreign to the European tradition, which privileged deductive analysis and proofs (Grattan-Guinness, 1992). Babbage realized that solving these algorithmic problems would necessitate a new kind of mechanical computer -- one that could be given a series of instructions without a determinate solution and iterate through the sequence until it computed the desired entry. Babbage’s mathematical study of chess inspired an entirely new algorithmic approach to European mathematics and laid the foundation for a theory of computation that would occupy the remainder of his career.
What might seem at first like a chance discovery was in reality a systematic research program spanning the first decade of Babbage’s mathematical career. Inspired by the work of German polymath Gottfried Wilhelm Leibniz, Babbage developed a “geometry of situation” that would allow for the mathematical study of the relationships between objects in space and through time, without the need to locate objects by their Cartesian coordinates. Leibniz’s “situations” were fully relativistic configurations of objects as a network of relations -- and indeed, his situational geometry would influence the development of graph theory, combinatorics, General Relativity, and topology (De Risi, 2007; De Risi, 2018). Babbage first mentions the geometry of situation in a preface to an 1813 text by the Analytical Society, his mathematical reformist club at Cambridge. In this preface, Babbage describes the geometry of situation as a theory at the boundaries of mathematics that is still in its infancy due to “the great difficulty of reducing its conditions into symbolic language” (Babbage and Herschel, 2013, p. xx). He notes only three applications of this theory -- Leibniz’s use of it to describe the board game solitaire, and Leonhard Euler’s and Alexandre-Theophile Vandermonde’s later elaboration of it through the study of the “Knight’s Tour” problem in the game of chess. By 1817, Babbage would join these venerable mathematicians in the study of this new geometry through games.
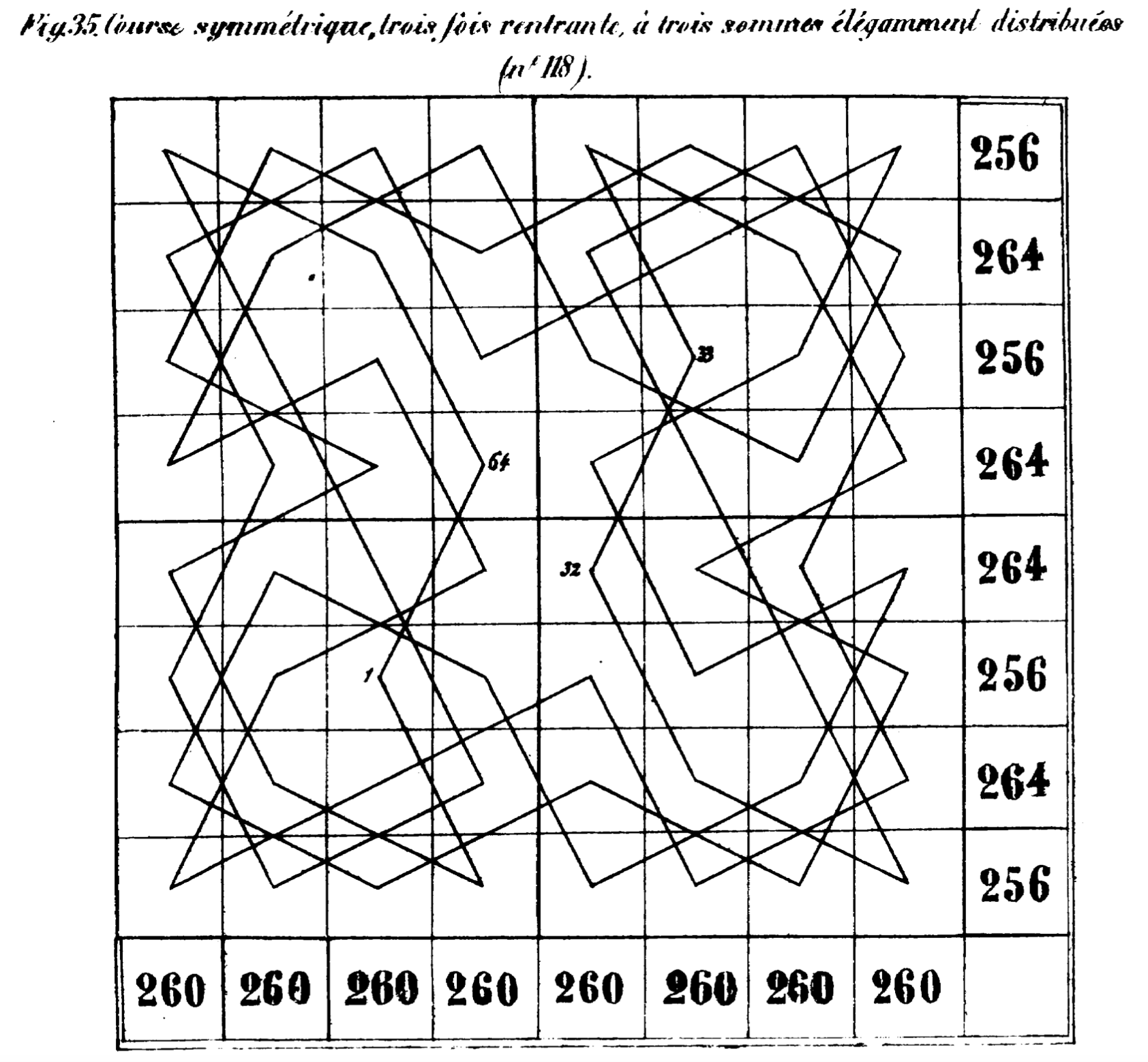
Figure 1. A representation of the Knight’s Tour around every square of the chessboard (Jaenisch 1862, Plate XVIII). Click image to enlarge.
Babbage’s short article on the Knight’s Tour problem laid the foundations for a unique “algorithmic” approach to mathematics that would characterize the rest of his career (Grattan-Guinness, 1992). Babbage was clear about the enormous implications of this work, noting that a solution to this puzzle would allow for “a general process applicable to [an entire] class of equations” which “open a wide field of analytical inquiry,” and present the possibility of novel approaches using mechanical calculation (Babbage, 2010, p. 218). This problem -- which dates to at least the ninth century in India -- was first mathematically formalized by Euler in 1766 and was further generalized by Vandermonde shortly afterwards [3]. Euler asked: Can a proof be constructed describing a route for a chess knight to land on each square of the board exactly once before returning to its starting square (Euler, 1766, p. 310)? Babbage’s approach was to construct an entirely new method of symbolic notation describing the set of knight’s moves as an ordinal sequence and appending any other move possibility to the actual move made. For instance, move 11 “communicates with” move 32 because the knight could have gone to either of these two squares interchangeably and still completed its tour (Babbage 1817, p.73). This symbolic notation allowed Babbage to establish a relationship between the spaces to which the knight jumped and the time sequence in which it made those jumps. It was a new language of space, time and action.
As can be seen in the quote above, Babbage openly credited his interest in this new “species” of problem to the study of chess. But even this sweeping proclamation does not fully capture the extent of his interest in games. In 1820, he published an essay concerning games of chance in which he notes that the series of problems he is considering are “not themselves dependent on chance” (Dubbey, 2004, p. 153). Instead, they are further elaborations of the geometry of situation. In the essay, he describes certain situations in games of chance where probability theory fails because it does not account for the “order of succession” in which events happen -- from repeated coin tosses to the selection of colored lottery balls from an urn (Babbage 1820, p. 154). To solve these problems, he again uses a symbolic description of event sequences that accounts for multiple possible “moves” (heads or tails for a coin or the different colored lottery balls). In the conclusion, Babbage notes that these problems “afford an instance of the immediate application of some very abstract propositions of analysis to a subject of constant occurrence, which […] I have preferred treating in particular instances, instead of investigating in its most general form” (Ibid., p. 177). His work on chess was merely one instance of a larger research program to construct a new geometry through the study of games.
While Babbage made good on his promise not to publish a general study of the geometry of situation, this was not due to any resolve on his part, but to historical exigency. He produced a manuscript in 1821-22 dedicated to the study of mathematical analysis (now housed in the British Library) that concludes with an essay dedicated to games; this essay, Babbage notes, “consists of a variety of problems requiring the invention of new modes of analysis” (Babbage, 1997). The manuscript utterly baffled his friend and editor of the Edinburgh Journal of Science, David Brewster, who told Babbage that he would not find a single reader who could understand it (Dubbey, 2004) However, the essays in this manuscript were widely known and quite influential among fellow English mathematical reformers at the time (Lambert, 2021). The analysis contained therein was of sufficient quality that historian J.M. Dubbey would conclude: “If he had developed the very fruitful ideas contained in the book […] it might well have been that mathematical philosophy, modern algebra, the theory of games and stochastic mathematics would have developed many decades before they actually did” (Dubbey, 2004, pp. 129-30). Babbage himself makes clear, however, that these ideas were further developed under the guise of a general theory of symbolic computation.
Babbage’s unpublished essay on games was an ambitious attempt to develop a complete geometry of situation through the analysis of games of all kinds. He begins by describing a class of questions entirely different from other modes of mathematical analysis, for which all current methods are insufficient: “The class of questions to which I allude chiefly comprise such as are referable to the Geometry of Situation and have very frequently arisen from games of skill” (Ibid., p. 126). Babbage’s stated objective in this essay is to develop a symbolic language for representing sequences and relative positions in games, and to outline the various difficulties and possibilities present in the various types of game. He alludes to Leibniz by suggesting that games share a privileged relationship with human ingenuity, and thus merit the organized pursuit of mathematicians [4]. He then divides games into categories, each with their own mathematical approach: games of pure chance are the province of the mathematics of probability; individual games like solitaire can be solved by reversing the series of moves taken (as Leibniz had previously described); games of mixed strategy and games of pure strategy presented a unique problem of describing symbolically the position of each move in a series relative to an opponent’s moves.

Figure 2. A later sketch by Babbage of his tic-tac-toe program [5]. Click image to enlarge.
Anticipating his design for a game-playing automaton later in life, Babbage pursues a solution to strategy games by presenting an equation of how to solve the game of tic-tac-toe. He finds a novel use for some of his earlier symbolic algebra by describing the full sequence of nine moves in a game of tic-tac-toe, where each move is described with respect to every other possible move. In other words, Babbage independently developed a search tree (see Figure 2) [6]. While the notation is unwieldy and the actual solution of an optimal strategy for tic-tac-toe was not attempted, the revolutionary nature of this project should not be understated. Dubbey describes it as “the first recorded stochastic process in the history of mathematics” (Dubbey, 2004, p. 129). Babbage is similarly confident in the efficacy of this new notational system. When he returns to the topic later in life, in his Passages from the Life of a Philosopher, he presents this system as a proof that an optimal strategy for all games of skill can be determined through computation (Babbage, 1864, pp. 465-471). In fact, this stochastic representation of tic-tac-toe makes it clear that Babbage had used games to devise general algorithms for mechanical computations before he first presented work on this new approach to computation in 1822. It was a program for the first ever computer game (Monnens, 2013).
Babbage’s subsequent reference to this project suggests that he had already conceived of a mechanical application to the geometry of situation in games. He analyzes games once again in 1821 while presenting his paper, “On the Influence of Signs in Mathematical Reasoning.” Games of chance and games of skill figure prominently in this essay, which argues for the efficacy of symbolic analysis in mathematics (Babbage, 1826b). He begins his discussion of games of skill by noting their importance for determining solutions to problems “where two parties successively make choice either of things or of situations” (Ibid., p. 19). Babbage argues that the only possible solutions for this class of problems result from an approach like his function mentioned above, which “enables us to delay the decision of the individuals actually selected until the conclusion; and thus by other means, to satisfy the other conditions of the problem” (Ibid., p. 20). In other words, he turns an undefined problem of assigning value to a sequence of choices into a finite calculation problem of determining how to arrive at a winning position in a game of skill.
It seems clear from Babbage’s subsequent discussion that his approach to this problem was intended to promote the unification of games and computation. He tips his hand when noting that he doubted this method could actually be successful, “until some more condensed method of indicating and to a certain extent also of executing such operations, shall have been contrived” (Ibid., p. 20). At the time he first presented this work, Babbage was actively devising a new method of mechanical notation (see discussion below) and a new means of calculating problems through mechanical computation. Thus, this statement is less wistful speculation and more a reference to his ongoing research program. The connection between games and mechanical calculation is reinforced in his conclusion: “The cause, on which its successful application depends, seems to be the power which it gives of uniting together a number of cases totally distinct, and of expressing them all by the same formula” (Ibid., p. 21). While Babbage restricts his early research of the geometry of situation to the analysis of abstract “situations” using symbolic mathematics, he would next develop a notation system for the function of mechanisms that borrowed from this earlier abstract geometry. As is clear from the statement above, he recognizes that this ludic geometry could be extended into a description of the relationships between any phenomena. The space, time and action sequences in game situations could function as a model of all situations.
The Perfection of Mechanical Reason
Babbage’s early efforts to develop a symbolic language for algorithmic sequences would later be instantiated into the design of the Analytical Engine. Influenced by the punch card programming of the Jacquard loom, he developed his own card programming system that would engage or disengage the various gears of the Engine depending on the patterns of holes in the card. Lovelace would later identify this punch card system as the chief innovation of the Engine due precisely to its symbolic representation of arithmetical relationships:
The bounds of arithmetic were however outstepped the moment the idea of applying the cards had occurred; […] In enabling mechanism to combine together general symbols in successions of unlimited variety and extent, a uniting link is established between the operations of matter and the abstract mental processes of the most abstract branch of mathematical science. A new, a vast, and a powerful language is developed […] for the purposes of mankind than the means hitherto in our possession have rendered possible. (Lovelace, 1843, p. 163)
Lovelace’s speculation on the power of symbolic computation was eerily prescient of its actual contributions to the sciences. As she describes, the innovative use of punch cards to represent numbers as variables (see Figure 3) unlocked an entirely new approach to mathematics. Operation cards could be inserted into the “store” of the Engine governed the different operations to be carried out (addition, multiplication, squaring) and variable cards specifying the operand numbers were then placed in the “mill.” Each card was stamped with a grid of holes that addressed the various gears and cogs of the machine -- in other words, the cards were abstract representations of the spatial and temporal relationships between the many components of the Engine.

Figure 3. Variable cards (left) and operation cards (right) for the Analytical Engine [7]. Click image to enlarge.
Babbage’s use of punch cards depended conceptually upon his prior analysis of situations in games. But he also made an intermediate innovation that allowed him to symbolically address the interlocking parts of a machine in the first place. He called it the “Mechanical Notation” -- a symbolic system of notation that describes the relative position of each piece of a machine at a given moment in time. This notation, which he first introduced in 1826, was intended to resolve the “difficulty of retaining in the mind all the contemporaneous and successive movements of a complicated machine, and the still greater difficulty of properly timing movements which had already been provided for” (Babbage, 1826a, p. 250). To illustrate the efficacy of this notation system, Babbage uses it to denote the movements of the components of a clock as they interact through time. Hinting at the greater importance of this work, Babbage concludes by noting: “The signs, if they have been properly chosen, and if they should be generally adopted, will form as it were an universal language […] and I have myself experienced the advantages of its application to my own calculating engine, when all other methods appeared nearly hopeless” (Ibid., p. 261). In early examples of this notation, the relative position of gears over time is depicted on the squares of a grid (see Figure 5).
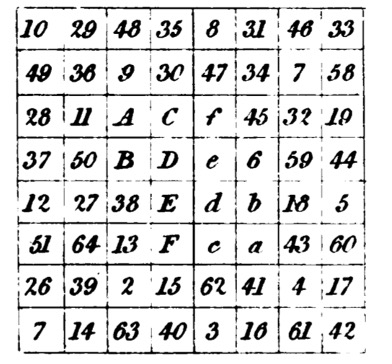
Figure 4. Symbols substituted for positions in Babbage’s Knight’s Tour article, (Babbage, 1817). Click image to enlarge.
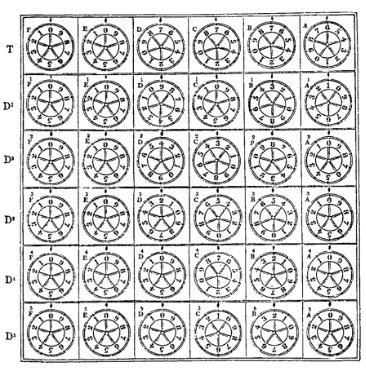
Figure 5. Spatial orientation of gears at different positions in time -- diagram of arithmetical operations in Babbage’s Difference Engine 1, 1834 (Babbage, 1989:2, p. 147). Click image to enlarge.
This suggestion of a universal symbolic notation again alludes to the work of Leibniz, which proved a persistent influence on Babbage’s work. A universal symbolic language was a centerpiece of Leibniz’s life’s work -- what Leibniz called a “universal characteristic&rdquo -- and found its way into nearly all his other endeavors, from formal logic and philosophy to linguistics and political science (Leibniz, 1989, pp. 221-228.). Babbage’s invocation of Leibniz’s universal language in the context of mechanics is not an idle one: Leibniz developed the geometry of situation with this very usage in mind. In his earliest collected reference to the geometry of situation -- a letter to mathematician Christiaan Huygens in 1679 -- he describes its potential for perfecting the science of mechanism:
I believe that, so far as geometry is concerned, we need still another analysis which is distinctly geometrical or linear and which will express situation [situs] directly […] And I believe that I have found the way and that we can represent figures and even machines and movements by characters, as algebra represents numbers or magnitudes. […] If it were completed in the way in which I think of it, one could carry out the description of a machine, no matter how complicated, in characters which would be merely the letters of the alphabet, and so provide the mind with a method of knowing the machine and all its parts, their motion and use, distinctly and easily without the use of any figures or models and without the need of imagination. (Leibniz, 1989, p. 250)
The uncanny similarity between Babbage’s rationale for his notation and Leibniz’s own reasoning becomes even more apparent when each discuss the possibilities of this new geometrical symbolism. Both of them see the abstract representation of mechanism as a way of optimizing the performance of mechanical calculations through mathematical analysis (Ibid., pp. 250-51). In other words, the geometry of situation represents a general theory of computation that allows one to solve problems algorithmically through the symbolic representation of mechanism.
The evidence for the connection between the geometry of situation and mechanical notation is in an essay by Vandermonde to which Babbage continually referred across his work. In “Remarques sur les Problèmes de Situation” (“Remarks on the Problems of Situation”), Vandermonde places Euler’s solution to the Knight’s Tour in the context of Leibniz’s broader study of situation in games. The notation described by Vandermonde, “made up of numbers which do not represent quantities, but ranks in space,” is logically consistent with Babbage’s more elaborate formula describing a solution to tic-tac-toe (Translation mine. Vandermonde, 1771, p. 566). It also closely resembles the complete version of Babbage’s Mechanical Notation described in 1851, where each piece (P) or arm (A) are assigned a number (e.g., 3P), described as a set of component “parts” (e.g., 3P1, 3P2, 3P3) which are themselves represented according to their location at each period in time (e.g., 3P1, 3P2, 3P3) (Babbage, 1989:3, p. 224). This precise symbolic description of interlocking mechanisms situated in time and space represents a development of the earlier geometry of situation pursued by Leibniz, Euler and Vandermonde. For Babbage, as for these other three, games served as models of spatiotemoral situations found in every other aspect of life.
In Babbage’s first description of the Analytical Engine in 1837, he is explicit about the stakes of this project, framing it as “the complete control which mechanism now gives us over number” (Babbage, 2013 [1837], p. 54). This control was achieved (in theory) by a meticulous project of making each physical component addressable by other components at any point in time (Dhaliwal, 2022b; Bromley, 1998). Babbage repeatedly emphasizes the importance of relying on “the perfect security and certainty” of the machine’s actions (Babbage, 2013 [1837], pp. 36-7; 48-9). It should be noted that these philosophical ambitions continually ran aground when Babbage attempted to actually instantiate his theory into working mechanical devices (Lindgren, 1990; Jones, 2016). But it is important to recognize that this vision of the mechanical perfection of reason, which occupied the better part of Babbage’s life, was the theoretical outcome of a study of games inspired by the writings of Leibniz.
When Leibniz formed the Berlin Academy of Sciences in 1710, the organization produced a journal of scientific writings, entitled the Miscellanea Berolinensia Ad Incrementum Scientiarum (The Berlin Miscellany for the Furtherance of the Sciences), to mark its founding. Two of Leibniz’s essays bookend the diverse topics discussed in this text. Placed prominently in the first section is his essay advocating for the formation of a general science of games, and the volume ends with his description of his “stepped reckoner” -- one of the earliest mechanical computers. The tissue connecting these concerns is the study of “games of situation” -- Leibniz’s term for strategy games [8]. Charles Babbage was the conscious successor to this tradition. His contributions to the history of computation were undergirded by a new sort of mathematics premised on the rules and regularities found in games.
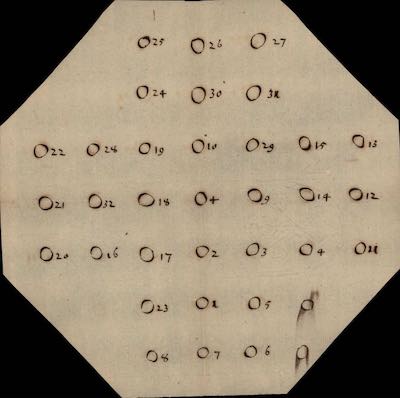
Figure 6. Mathematical treatment of solitaire in Leibniz’s notebooks [9]. Click image to enlarge.
Leibniz not only constructed his geometry of situation around the game of solitaire, but also invented his own game called “reverse solitaire” to model his theory of the creation of the universe (Leroux, 2015). In this reversal of the traditional rules, the board begins with a single marble at the center, and each leap adds rather than removes a marble from the board. He speculated that the algorithmic steps involved in producing geometrical figures could constitute its own form of geometry (Leibniz, 1710). Coincidentally, the game of solitaire also inspired Lovelace’s first experiments with algorithms three years before her first computer program. On February 16, 1840, Lovelace wrote a letter to Babbage alluding to a prior conversation with him concerning his study of chess and suggesting that the game of solitaire could also be a topic of mathematical analysis -- unaware that Leibniz’s study of solitaire prompted Babbage’s entire work on games. She explains:
My Dear Mr Babbage. Have you ever seen a game, or rather puzzle, called Solitaire? […] I want to know if the problem admits of being put into a mathematical Formula, & solved in this manner. […] There must be a definite principle, a compound I imagine of numerical & geometrical properties, on which the solution depends, & which can be put into symbolic language. […] I have numbered the holes in my drawing for the sake of convenience of reference. (Lovelace, 1840, pp. 82-83)
Lovelace’s description of an algorithm for solving solitaire evinces the fact that, as with Babbage, she first modeled programs as abstract sequences of moves on a game board before penning algorithms for the Analytical Engine. Further archival research has identified pen sketches by Babbage of several of Leonhard Euler’s situational puzzles, with attempted solutions traced in pencil by Lovelace (Hollings, Martin & Rice, 2018, pp. 89-96). These findings provide us a rare view of the two inventors communicating through play. Lovelace hints at this earlier connection between games and computers in her 1842 notes when she compares the store of the Engine to “a pile of rather large draughtsmen heaped perpendicularly one above another” (Lovelace, 1843, p. 165). Her subsequent education in mathematics afforded her a symbolic language for formalizing the first computer algorithms, but only after she had already explored these spatiotemporal relationships in ludic practice.
Leibniz developed his geometry of situation in the wake of European probability theory and the ideology of certainty and reason that followed in its wake. Probability theory itself was modeled upon games of chance: mathematics prodigy Blaise Pascal corresponded with fellow mathematician Pierre Fermat on the equitable outcome of an interrupted dice game and through so doing imagined the universe itself as a fair game (Campe 2013). As Pascal later summarized, “the uncertainty of fortune is so restrained by the equity of reason, that each of two players can always be assigned exactly what is rightly due. […] the doubtful outcomes of the lot […] has not been able to escape the dominion of reason” (Quoted in: Franklin, 2001, p. 312). This intellectual development -- what historian of science Ian Hacking has called the “taming of chance” -- had a seismic impact on the knowledges and societies of early modern Western Europe [10]. In his exacting specifications for a computational machine that eliminated any uncertainty of outcome, Babbage saw himself as an evangelist of this dominion of reason.
While Pascal described reason’s conquest of chance, Babbage saw in computation the potential to transmute space into time and back: “[I]t appears that the whole of the conditions which enable a finite machine to make calculations of unlimited extent are fulfilled in the Analytical Engine […] I have converted the infinity of space, which was required by the conditions of the problem, into the infinity of time” (Babbage, 2013 [1837], p. 13). This pronouncement posits the geometry of situation’s logical conclusion, which forged a relationship between space and time through the function of mechanism. Merely three years after her first scribblings on gameboards and puzzles, Lovelace fully understood the implications of this new science: it could describe “those unceasing changes of mutual relationship which, visibly or invisibly, […] are interminably going on in the agencies of the creation we live amidst” (Lovelace, 1843, p. 163). With this she declared the fulfillment of Leibniz’s dream.
Anticipation and Learning
To fully appreciate the constitutive role that games played in Babbage’s and Lovelace’s computational thinking, it is important to distinguish which formal aspects of games led to which developments. As Babbage clarified in his brief taxonomy of games quoted above: games of chance help to express probabilities, individual (puzzle) games like solitaire provide an opportunity for descriptions of sequence, but only games of skill like chess or tic-tac-toe model conditional if-then logics and branching complexity. Perhaps for this reason, Babbage maintained an interest in games of skill until the end of his life. One of his last attempts to secure funding for the assembly of the Analytical Engine was a planned construction of a game-learning automaton -- intended initially to play chess, but later conceived as a tic-tac-toe automaton due to the complexity of the former. In his memoir, Passages from the Life of a Philosopher, he describes a basic conditional algorithm for a machine that can account for the gameplay moves of an opponent and look ahead two or three moves to calculate the outcome of these moves (Babbage, 1864, p. 465). Summarizing the central principles of the automaton, he notes: “Now I have already stated that in the Analytical Engine I had devised mechanical means equivalent to memory, also that I had provided other means equivalent to foresight, and that the Engine itself could act on this foresight” (Ibid., p. 467). What characterized the automaton’s function were the two traditionally human capacities of memory and foresight, which are necessitated by the conditional logics and branching complexity of games of skill.
The other means of foresight to which Babbage refers is the mechanism of the “anticipating carry” (Ibid., p. 63). While Lovelace declared the punch cards to be the central invention of the Analytical Engine, Babbage himself was proudest of the anticipating carry. He realized when measuring the calculation time of the Engine that by far the least efficient process was the sequential transfer of digit “carries” from gear to gear -- for example, when 9,999 adds up to 10,000, the final unit would have to register across five different gears. His mechanical solution was a wire connecting all the gears that slotted into place when a given gear shifted to 9. When any of these 9s increased further, this wire would simultaneously propagate the carry across the entire sequence of 9s. The efficiency gain of the anticipating carry was so great that it was the initial impetus behind the division of the Engine into a store (that delivered the instructions) and a mill (that made the calculations themselves) (Jones, 2016, p. 54). While in his memoirs Babbage ascribes mechanical foresight to both the carry mechanism and his game program, it is clear from this survey of his early work that the latter far predates the former. This example helps to illustrate the unique affordances of games of skill for the central innovations of the Analytical Engine.
And what of this capacity to learn? There is evidence that this too was inspired by games of skill. In 1819 and again in 1820, Babbage recorded in his journals that he attended a demonstration of a popular chess automaton, the “Mechanical Turk,” playing and losing to it on the second occasion (Standage, 2002, pp. 137-145). This device, which was purportedly a chess-playing automaton but in reality concealed a skilled chess player manipulating levers from the inside, was invented by Wolfgang von Kempelen in the eighteenth century and was toured across Europe and even America by Johann Maelzel throughout the nineteenth century (Ibid., p. 103). Numerous historians have suggested that this device modeled for Babbage the possibility that automata could one day play chess -- a proposition he later made in his Passages -- and that it perhaps inspired the Analytical Engine itself [11]. While his bout with the automaton happened well into his research into games, it is significant that he drafted his essay on games of skill a year after this event. Thus, it is plausible that even the memory capacity of the Analytical Engine was inspired by his speculations on the unique affordances of games of skill.
I want to suggest here a more intimate relationship between games and computation in Babbage’s project than is usually acknowledged: Babbage was concerned not only with the fact that an automaton could play games, but also with the mathematics necessary to optimize the solution to problems that required the coordination of elements into spatial and temporal relationships. In other words, games were not simply a convenient topic for the development of the geometry of situation. The precise rules, concepts and mechanics of games were necessary antecedents to the development of an entire mode of mathematical analysis. For Babbage to develop this theory independently of games, he would have needed to stumble upon a problem that involved a turn-based agonistic encounter between two or more parties where items were placed in abstract space in a linear sequence for the pursuit of a measurable and finite outcome. For many scholars of games, these properties are the very definition of a game [12]. The geometry of situation points to a capacity of games that has less to do with the modality of play and more with the structure they impose as model systems.
Babbage turns again to games as models of computing technology in his plans for a tic-tac-toe automaton. As described in his Passages, this project first occurred to him as a means of demonstrating “the power which I possessed over mechanism through the aid of the Mechanical Notation” (Babbage, 1864, p. 465). After taking to the streets to assess whether it was commonly believed that games of skill required human reason, Babbage endeavored to demonstrate that “every game of skill is susceptible of being played by an automaton” (Ibid., p. 466). His initial theoretical approach focused on describing chess strategy using chains of conditional logic: “Is the position of the men […] consistent with the rules of the game? If so, has Automaton himself already lost the game? […] If not, can he win it at the next move? If so, make that move” (Ibid., pp. 466-7). When reflecting on the reaction his audiences might have to an automaton who mastered a game of skill, he waxes philosophical, noting it to be “worthy of remark how admirably this illustrates the best definitions of chance by the philosopher and the poet,” that, quoting scientist Pierre-Simon Laplace, “Chance is but the expression of man’s ignorance” (as cited in Babbage, 1864, pp. 469-70). This philosophical objective reiterates that historically specific game forms like chess and tic-tac-toe modeled computing technologies before those technologies existed.
Although Babbage and Lovelace’s plans to complete a working Analytical Engine never came to fruition, their concepts and designs cast a long shadow over the later history of computing, inspiring the work of a wide range of early computer scientists and engineers [13]. Babbage’s reflections on the implications of the mechanization of labor processes for political economy also had a profound influence on the technological theory of Karl Marx, whom Simon Schaffer calls “Babbage’s most penetrating London reader” (Schaffer, 1994, p. 205). Schaffer clarifies that the Analytical Engine’s capacities of anticipation and memory “were profound resources for Babbage’s metaphysics and his political economy” (Ibid., p.207). Indeed, some of the most influential neoclassical economists leaned on Babbage in their work, including Alfred Marshall, William Stanley Jevons, John Stuart Mill and Joseph Schumpeter (Cooke, 2005; Niman, 2008; Rosenberg, 2000). Marshall and Jevons in particular employed Babbage’s chess automaton as a model of rational economic man through its capacity to anticipate and learn from mistakes (Raffaelli, 1994; Jevons, 1883). The use of games to model symbolic computation did not end with the Analytical Engine, but intensified throughout the twentieth century (Pizelo, 2024a; Pizelo, 2024b). In our moment, games have become the paradigmatic environment for the study of machine intelligence (Yannakakis and Togelius, 2018). This, too, is part of the history of games.
Conclusion
Games played computers before computers played games. This simple observation has profound implications for how we tell histories of our moment. It inverts the traditional prioritization of computers as the condition of possibility for games. It also emphasizes the epistemological capacities of games as models and suggests a future research program to identify other cultural logics influenced by games (Fuchs et al., 2014; Stark, 2024). If computers were themselves dependent on game logics, then Eric Zimmerman’s influential description of our “Ludic Century” is further intensified by including the “Information Age” as well [14]. The reversal of the historical relationship between games and computation prompts further questions regarding the construction of game studies as a discipline: If the historical development of electronic computation belongs to the history of games, how should game scholars configure the relationship between “analog” and “digital” games, or “board” and “video” games? How can histories of games help to denaturalize the Euro-American project of perfecting “reason”? How might game researchers contextualize the operational logics of computing technologies differently if we recognize that these same logics were at work in ancient media (Pizelo, 2023)? Does game studies have new perspectives, new concepts and new vocabulary to offer theorists of computation and digital media seeking to describe the spatial and temporal orders imposed by procedural rules (Galloway, 2006; Wark, 2007; Bogost, 2010)?
The many games Babbage studied -- including chess, solitaire, dice games and tic-tac-toe -- were not found objects, they were built objects. They are technologies with their own histories, cultures and communities. An appreciation for the influence of the material technologies of games necessitates both an acknowledgement of the things games themselves build and the writing of new histories emphasizing the entanglements between games and the phenomena they model. Game studies, in its generative interdisciplinarity, is well positioned for this task (Chess and Consalvo, 2022; Gecker, 2021; Deterding, 2017). How will the study of our moment change if we learn new ways of describing the generative logics of games? Can we build new systems? Charles Babbage and Ada Lovelace believed so.
Acknowledgements
I would like to thank Ranjodh Singh Dhaliwal in particular for his early provocations and later conversations on the enduring relevance of Babbage and Lovelace. Con Diaz and David Dunning were both so helpful when I was getting a feel for histories of computing and mathematics. Ryan Wright, Doug Stark and Kate Hayles were early readers that encouraged me to be bolder with my intervention. Colin Milburn, Stephanie Boluk and Patrick LeMieux all helped this article to take shape. In addition, the members of SIGCIS were helpful commentors on an earlier presentation of my argument. Finally, I want to acknowledge the formative critique of the anonymous reviewers and the meticulous work of the journal editors.
Endnotes
[1] See in particular; Pias, 2017; Malaby, 2007; Crogan, 2011; Milburn, 2015; Milburn, 2018; Jagoda, 2020. For a theory of scientific modeling as a game of make-believe, see; Toon, 2012. For games as modeling technologies, see; Möring, 2013; Wardrip-Fruin, 2020. There is also a rich tradition of scholarship on the role of games in education and pedagogy. For an introduction to this topic, see; Gee, 2003; Brougère, 1999.
[2] “A series of cube numbers might be formed, subject to this condition, that whenever the number 2 occurred in the tens’ place, that and all the succeeding cubes should be increased by ten. In such a series, of course, the second figure would never be a 2, because the addition of ten would convert it into 3.” Ibid., p. 218.
[3] For a discussion of the earliest solutions to the Knight’s Tour which were used to compose Sanskrit poetry, see; Murthy, 2020. Before his published essay on the Knight’s Tour, Euler mentions the problem in a 1757 letter to Christian Goldbach. See; Zubkov, 2010.
[4] Leibniz made frequent statements to this effect throughout his lifetime correspondence. See; Leibniz, 1996, pp. lxiv-lxv.
[5] Babbage, Charles. “Scribbling Book Volume XIV,” The Babbage Papers at the Science Museum, London. p. 98. CC BY-NC-SA 4.0 License.
[6] For Ernst Zermelo’s influential search tree notation, see; Schwalbe and Walker, 2001.
[7] Babbage, Charles. “Punched cards for Babbage's Analytical Engine,” The Babbage Papers at the Science Museum, London. CC BY-NC-SA 4.0 License.
[8] Leibniz goes into depth on his taxonomy of games and the mathematical study thereof in a letter to fellow probability theorist Pierre Rémond de Montmort. See; Leibniz, 1989, p. 487.
[9] Image taken from the Gottfried Wilhelm Leibniz Bibliothek, Niedersächsische Landesbibliothek, Leibniz-Handschriften zur Technica, LH 38, fol. 195 v. http://digitale-sammlungen.gwlb.de/resolve?id=00068537.
[10] Hacking, 1990. For the development of the theory of probability through games and its ramifications, see also; Daston, 1995; Campe, 2013.
[11] For a recent discussion of this relationship, see; Dhaliwal, 2022a, pp. 377-409. See also; Schaffer, 1999; Schwartz, 2019.
[12] For a recent survey of definitions of games, see; Consalvo and Paul, 2019. For chess and the history of algorithm, see; Larson, 2018.
[13] Babbage had a clear influence on the later designs of Percy Ludgate, the automata of Leonardo Torres y Quevedo, the analytical engine of Louis Couffignal, as well as a cadre of post-WWII engineers, including Howard Aiken, William Phillips, Vannevar Bush, Konrad Zuse, and others. See; Randell, 2013, pp. 15-17. I am indebted to Ranjodh Singh Dhaliwal for alerting me to the broader economic influences of Babbage’s work, especially on Karl Marx.
[14] Zimmerman, 2015. In 1997, historian Colas Duflo dubbed the eighteenth century “le siècle du jeu,” that is, “the century of games and play.” Peter Burke has recently depicted a similarly central role for play during the Renaissance. Johan Huizinga found play to be an explanatory mechanism for the culture of the late Middle Ages long before he generalized this methodology in Homo Ludens. If we take a global perspective, our list of “ludic centuries” would quickly expand further. See; Duflo, 1997; Burke, 2021; Huizinga, 1996 [1921].
References
Babbage, C. (1817). “An Account of Euler's Method of Solving a Problem, Relative to the Move of the Knight at the Game of Chess,” The Journal of Science and the Arts, 3(5), 72-7.
Babbage, C. (2010 [1889]). Babbage's Calculating Engines: Being a Collection of Papers Relating to Them; Their History, and Construction. Babbage, Henry P. ed. Cambridge University Press.
Babbage, C. (1997). “Essays on the Philosophy of Analysis,” Correspondence and Scientific Manuscripts from the British Library, London. Reel 21. Adam Matthew Publications.
Babbage, C. (1826a). On the Influence of Signs in Mathematical Reasoning. J. Smith, printer to the University.
Babbage, C. (1826b). “On a Method of Expressing by Signs the Action of Machinery,” Philosophical Transactions of the Royal Society of London. 250-265.
Babbage, C. (2013). “On the Mathematical Powers of the Calculating Engine 1837,” in: Randell, Brian, ed. The Origins of Digital Computers: Selected Papers. Springer.
Babbage, C. (1864). Passages from the Life of a Philosopher. Longman, Green, Longman, Roberts, & Green.
Babbage, C. (1989). The Works of Charles Babbage (Vols. 2 and 3, M. Campbell-Kelly Ed.). London, Pickering & Chatto.
Babbage, C. & Herschel, J. (2013 [1813]). Memoirs of the Analytical Society. Cambridge University Press.
Bogost, I. (2010). Persuasive Games: The Expressive Power of Videogames. MIT Press.
Bromley, A. G. (1998). “Charles Babbage's Analytical Engine, 1838.” IEEE Annals of the History of Computing 20(4), 29-45.
Brougère, G. (1999). “Some Elements Relating to Children’s Play and Adult Simulaton/Gaming.” Simulation & Gaming, 30(2), 134-146.
Burke, P. (2021). Play in Renaissance Italy. Polity Press.
Campe, R. (2013). The Game of Probability: Literature and Calculation from Pascal to Kleist. Stanford University Press.
Chess, S. & Consalvo, M. (2022). “The Future of Media Studies is Game Studies,” Critical Studies in Media Communication, 39(3), 159-164.
Consalvo, M. & Paul, C. A. (2019). Real Games: What's Legitimate and What's not in Contemporary Videogames. MIT Press.
Cook, S. (2005). “Minds, Machines and Economic Agents: Cambridge Receptions of Boole and Babbage.” Studies in History and Philosophy of Science Part A, 36(2), 331-350.
Crogan, P. (2011). Gameplay Mode: War, Simulation, and Technoculture. U of Minnesota Press.
Daston, L. (1995). Classical Probability in the Enlightenment. Princeton University Press.
De Risi, V. (2018). “Analysis Situs, the Foundations of Mathematics and a Geometry of Space.” The Oxford Handbook of Leibniz.
De Risi, V. (2007). Geometry and Monadology: Leibniz's Analysis Situs and Philosophy of Space. Springer Science & Business Media.
Deterding, S. (2017). "The Pyrrhic Victory of Game Studies: Assessing the Past, Present, and Future of Interdisciplinary Game Research." Games and Culture 12(6), 521-543.
Dhaliwal, R. S. (2022a). “The Cyber-Homunculus: On Race and Labor in Plans for Computation,” Configurations 30(4), 377-409.
Dhaliwal, R. S. (2022b). “On Addressability, or What Even Is Computation?,” Critical Inquiry 49(1), 1-27.
Diaz, G. C. (2020). “Encoding Music: Perforated Paper, Copyright Law, and the Legibility of Code, 1880-1908.” Case Western Reserve Law Review, 71(2), 627-665.
Dubbey, J. M. (2004). The Mathematical Work of Charles Babbage. Cambridge University Press.
Duflo, C. (1997). Le Jeu: De Pascal à Schiller, Presses Universitaires de France (Paris).
Dunning, D. E. (2020). Writing the Rules of Reason: Notations in Mathematical Logic, 1847-1937 [Doctoral dissertation, Princeton University].
Essinger, J. (2014). Ada's Algorithm: How Lord Byron's Daughter Ada Lovelace Launched the Digital Age. Melville House.
Euler, L. (1766). “Solution d’une Question Curieuse que ne Paroit Soumise à Aucune Analyse,” Euler Archive - All Works. https://scholarlycommons.pacific.edu/euler-works/309
Fickle, T. (2019). The Race Card: From Gaming Technologies to Model Minorities. New York University Press.
Franklin, J. (2001). The Science of Conjecture: Evidence and Probability before Pascal. Johns Hopkins University Press.
Fuchs, M., Fizek, S., Ruffino, P., & Schrape, N. (2014). Rethinking Gamification. Meson Press.
Galloway, A. R. (2006). Gaming: Essays on Algorithmic Culture. U of Minnesota Press.
Galloway, A. R. (2021). Uncomputable: Play and Politics in the Long Digital Age. Verso Books.
Gee, J. P. (2003). “What Video Games Have to Teach Us about Learning and Literacy.” Computers in Entertainment (CIE), 1(1), 20-20.
Gekker, A. (2021). "Against Game Studies." Media and Communication, 9(1), 73-83.
Grattan-Guinness, I. (1992). “Charles Babbage as an Algorithmic Thinker,” IEEE Annals of the History of Computing, 14(3), 34-48.
Hacking, I. (1990). The Taming of Chance. Cambridge University Press.
Hollings, C., Martin, U. & Rice, A. C. (2018). Ada Lovelace: The Making of a Computer Scientist. Bodleian Library.
Huizinga, J. (1996). The Autumn of the Middle Ages (R. J. Payton & U. Mammitzsch, Trans.) University of Chicago Press. (Original work published 1921)
Jagoda, P. (2020). Experimental Games: Critique, Play, and Design in the Age of Gamification. University of Chicago Press.
Jaenisch, C. F. (1862). Traité des Applications de Analyse Mathématique au Jeu des Échecs. (Vol. 2). Imperial Academy of Sciences.
Jevons, W. S. (1883). Methods of Social Reform: And Other Papers. Macmillan and Company.
Jones, M. L. (2016). Reckoning with Matter: Calculating Machines, Innovation, and Thinking about Thinking from Pascal to Babbage. University of Chicago Press.
Lambert, K. (2021). Symbols and Things: Material Mathematics in the Eighteenth and Nineteenth Centuries. University of Pittsburgh Press.
Larson, M. (2018). “Optimizing Chess: Philology and Algorithmic Culture,” Diacritics, 46(1), 30-53.
Leibniz, G. W. (1710). Miscellanea berolinensia ad incrementum scientiarum, ex scriptis Societati Regiæ Scientiarum, exhibitis edita: cum figuris æneis et indice materiarum. Johan. Christ. Papenii. 22-26.
Leibniz, G. W. (1996). New Essays on Human Understanding, Bennett, Jonathan and Peter Remnant, eds., Cambridge University Press.
Leibniz, G. W. (1989). Philosophical Papers and Letters: A Selection (Vol. 2, L. E. Loemker, Ed.), Kluwer Academic Publishers.
Leroux, V. (2015). Le jeu dans la pensée de Leibniz [Master's thesis, l'Université Paris sciences et lettres].
Lovelace, A. A. (2015). “1842 Notes to the Translation of the Sketch of the Analytical Engine.” Ada User Journal, 36(3), 152-180.
Lindgren, M. (1990). Glory and Failure: The Difference Engines of Johann Müller, Charles Babbage and Georg and Edvard Scheutz (C. McKay, Trans.). MIT Press.
Malaby, T. M. (2007). “Beyond Play: A New Approach to Games.” Games and Culture, 2(2), 95-113.
Milburn, C. (2015). Mondo Nano: Fun and Games in the World of Digital Matter. Duke University Press.
Milburn, C. (2018). Respawn: Gamers, Hackers, and Technogenic Life. Duke University Press.
Monnens, D. (2013). “'I commenced an examination of a game called ‘tit-tat-to’': Charles Babbage and the 'First” Computer Game.' Proceedings of DiGRA 2013: DeFragging Game Studies.
Möring, S. M. (2013). Games and Metaphor - A Critical Analysis of the Metaphor Discourse in Game Studies. [Doctoral dissertation, IT University of Copenhagen]. Pure.itu.dk.
Murthy, G. S. S. (2020). “The Knight’s Tour Problem and Rudrata’s Verse: A View of the Indian Facet of the Knight’s Tour,” Resonance, 5(8), 1095-1116.
Niman, N. B. (2008). “Charles Babbage's Influence on the development of Alfred Marshall's Theory of the Firm.” Journal of the History of Economic Thought, 30(4), 479-490.
Pias, C. (2017). Computer Game Worlds (V. A. Pakis, Trans.). Diaphanes.
Pizelo, S. (2023). “Philosophy is an Egyptian Game: How Ancient Game Logics Structure our Present,” ROMchip 5(2).
Pizelo, S. (2024a). “Games and the Rise of Systems Thinking: From Models to Machines,” Representations 165(1), 92-119.
Pizelo, S. (2024b). Modeling Revolution: A Global History of Games as Model Systems. [Doctoral dissertation, University of California, Davis].
Randell, B. (2013). The Origins of Digital Computers: Selected Papers. Springer.
Rabouin, D. (2020). “Exploring Leibniz’s Nachlass at the Niedersächsische Landesbibliothek in Hanover,” European Mathematical Society Magazine, (116). 17-23.
Raffaelli, T. (1994). “The Early Philosophical Writings of Alfred Marshall.” Research in the History of Economic Thought and Methodology, 4, 51-158.
Rosenberg, N. (2000). “Charles Babbage in a Complex World.” Complexity and the History of Economic Thought: Perspectives on the History of Economic Thought. Colander, David, ed. Routledge. 47-57.
Schaffer, S. (1994). “Babbage's Intelligence: Calculating Engines and the Factory System.” Critical Inquiry, 21(1), 203-227.
Schaffer, S. (1999). “Enlightened Automata,” Clark, William, Jan Golinski, and Simon Schaffer, eds. The Sciences in Enlightened Europe. 126-165.
Schwalbe, U. & Walker, P. (2001). "Zermelo and the Early History of Game Theory." Games and Economic Behavior, 34(1), 123-137.
Schwartz, O. (2019). “Untold History of AI: When Charles Babbage Played Chess with the Original Mechanical Turk,” IEEE Spectrum Tech Talk. https://spectrum.ieee.org/tech-talk/tech-history/dawn-of-electronics/untold-history-of-ai-charles-babbage-and-the-turk
Standage, T. (2002). The Turk: The Life and Times of the Famous Eighteenth-Century Chess-Playing Machine. Walker & Company.
Stark, D. (2024). “Games as Epistemic Mediators: Rethinking Gamification with Morgenstern, von Neumann, and Bateson.” Configurations, 32(2), 93-109.
Toole, B. A. (1998). Ada, the Enchantress of Numbers: Prophet of the Computer Age, a Pathway to the 21st Century. Critical Connection. Strawberry Press.
Toon, A. (2012). Models as Make-Believe: Imagination, Fiction and Scientific Representation. Palgrave Macmillan.
Trammell, A. (2023). Repairing Play: A Black Phenomenology. MIT Press.
Vandermonde, Alexandre-Théophile (1771). “Remarques sur les Problèmes de Situation,” Mémoires de L’Académie Royale des Sciences (Paris) 2. 566-574.
Wardrip-Fruin, N. (2020). How Pac-Man Eats. MIT Press.
Wark, M. (2007). Gamer Theory. Harvard University Press.
Yannakakis, G. N. & Togelius, J. (2018). Artificial Intelligence and Games. Springer.
Zimmerman, E. (2015). “Manifesto for a Ludic Century.” The Gameful World: Approaches, Issues, Applications. MIT Press. 19-22.
Zubkov, A. M. (2011). Euler and Combinatorial Calculus. Proceedings of the Steklov Institute of Mathematics, 274(Suppl 1), 162-168.