The Games Economists Play - Implications of Economic Game Theory for the Study of Computer Games
by Jonas Heide SmithAbstract
It is a source of confusion that economists for decades have worked on "game theory" while studying economic behaviour. However, while not focused on games in the recreational sense this perspective does provide a highly meticulous complementary framework for the understanding of computer game structure and player behaviour. This article attempts to extract useful analytic concepts and insights from economic game theory and to give suggestions for how these might be put to concrete use in the study of computer games. A non-technical introduction is given, the framework is applied to computer games, a brief case study is performed and finally ideas for future research are presented.
Introduction
Studying games, as Jesper Juul (2001) puts it, is a "repeatedly lost art." There are those, however, who for the last many decades have devoted careers to the study of games in a somewhat special sense. These individuals, known to their peers as game theorists, can be said to have placed computer game theorists in a hard spot. Since the label is occupied, it is only by risking confusion that the term game theory can be used as a label for work on electronic entertainment of the ludic persuasion. What, then, do these economic game theorists do?
Imagine, for instance, two children sharing a cake. The rule is that the one who does not cut the cake gets to choose first. Now, assume that the cutter wants to maximize his share of cake and that he expects the other child to share this preference. He will do his best to cut the cake exactly in half.
Such an analysis, although extremely simple, implies a game theoretical perspective. We assume that the people involved desire the best possible personal outcome and are aware (on some level) of the perspectives of the other participants. By "game" we are not referring to any recreational sense of the word but to strategic interaction between agents ("game theory," henceforth, refers to this special perspective).
Phrased in such general terms, game theory is as old as social theory. In an informal version, but one logically akin to modern thinking, it found application in the study of human behaviour among the so-called contract theorists Thomas Hobbes (1588-1679), John Locke (1632-1704) and Jean-Jacques Rousseau (1712-1778) as they discussed the rationale behind individuals drawing up a "social contract." And it has seen use among a variety of writers attempting to analyse successful gambling strategies.
More formally, we can think of game theory as the systematic study of the relationship between rules, choice and outcome in competitive situations. Two main branches exist. Analytical game theory is the analysis of games played by non-empirical players; that is "ideal" players who may be endowed with any characteristics, which can be modelled. These players need not accurately correspond to real-world people and such work is only open to critique to the extent that the math involved is wrong. They are experiments in logic, not models of the real world. On the other hand, behavioural game theory is the study of actual human players as they are confronted with precisely defined games. In this branch, researchers study how people make choices and navigate social conflicts (Camerer, 2003).
The birth of game theory in its modern form is commonly said to be the publication of Johan Von Neumann and Oskar Morgenstern's Theory of Games and Economic Behaviour in 1944. The ideas put forth in this volume relied on complex mathematics with the ambitious goal of providing a solid scientific foundation for the discipline of economics. This work was expanded upon in the years to follow, reaching political science in the late 1960s and evolutionary biology in the early 1970s.
This article is split in three parts. First, key issues and concepts in game theory are introduced. Second, the general implications of applying a game theoretical framework to games are presented and discussed. And finally, a case study of the strategy game Age of Kings (1999) is made, exemplifying how game theory may be applied in the analysis of games.
Key Concepts in Game Theory
This section introduces game theory focusing on those issues, which are most relevant to computer game studies. The format here is informal in the attempt to impart the logic of the perspective rather than the exact details. The next section will relate the issues to computer games.
Game theorists attempt to provide precise descriptions of situations of conflicting interests in order to study the behaviour that such a conflict would (or, in some cases, should) elicit from rational agents. Players are assumed to consider the position and perceptions of other players while forming their strategies. Alternatively, players may be seen as merely thoughtlessly adapting their strategies over time. The latter is assumed when games are played between non-human actors (algorithms, bacteria, etc.). The games studied by game theorists are usually those in which players are unable to enter into binding agreements. This branch is known as non-cooperative game theory and constitutes by far the larger portion of the entire field.
Technically, a strategy here is a plan for dealing with all possible actions of other players. I will return to the concept of strategy below in the discussion of how game theoretical concepts map onto computer games. As opposed to less sophisticated conceptions of human behaviour, game theory is decidedly social. In human conflict situations there is rarely one context-independent best strategy. What works well depends on the actions of others. And since these actions depend on perceptions, game theory takes into account that agents expect each other to have certain interests, and to do their best to attain them.
In order not to confuse issues, there is an important distinction to be made between payoff (measured in points, dollars or the like) and the personal joy gained through a game. The game theoretical concepts described in the following make sense in relation to game-internal payoff only. When considering pay-off in a broader sense, things become much more complex. For instance, one may consider it quite a victory to last for 30 moves against a Chess grandmaster. Or imagine introducing a favourite board game to a child. In this case, one may actually want to lose the first round in order to encourage the child's interest. Also, in darkened arcades many Space Invaders players will have considered their scores highly gratifying even though the game may be technically impossible to win.
Thus, when trying to explain and predict actual player behaviour one may have to examine the personal motivations of players for doing what they do. A somewhat simplistic way of understanding the scope of (analytical) game theory as regards computer games would be to say that it applies to the extent that players try to achieve the goals presented by the game. It is crucial to remain aware that the "rationalism" implied in the approach is at best a useful approximation and that the accompanying assumptions about player behaviour are non-trivial.
Four characteristics of games are of particular interest: 1) The number of players, 2) the sum type, 3)whether the game is repeated and 4) the existence and type of equilibria.
Number of Players
Game theory works with either two-person games or games with more than two players, termed n-player games. An important difference between the two types, apart from the complexity of the mathematics involved, is the fact that coalitions may form between players of n-person games affecting the game dynamics. Since we are concerned with opposing interests, a player in this perspective needs not be a single person but can be a nation, a football team or a pair of Bridge partners.
In certain cases, game theory addresses situations where a single agent is effectively playing against the environment or "nature." In these so-called parametric models or "games against nature," the player is trying to optimize his or her outcome against an opponent who is oblivious to the player's choices. However, such situations are only indirectly thought of as within the domain of game theory as they are the subjects of standard economics.
The most famous among the key two-person games is "The Prisoner's Dilemma"-- "the game that launched a thousand studies" (Kollock, 1998 p.185; see also Axelrod, 1984 ; for a popular account see Poundstone, 1992). The game, explained below, is often considered a fundamental model for the study of conflict and its simplicity and potential scope has earned it a place in textbooks within a truly wide range of fields (Smith, 2002). Briefly, the Prisoner's Dilemma is a situation in which two people are faced with a temptation to act in their personal interest disregarding the interest of the other person. However, if they both choose this (individually rational) course of action they will both be worse off than if they had cooperated.
This well-known game is illustrated below. Each player, let's call them Bob and Alice, must choose between one of two options: Cooperate or defect.
| Alice | |||
| Cooperates | Defects | ||
| Bob | Cooperates | Bob: 3 points Alice: 3 points |
Bob: 0 points Alice: 5 points |
| Defects | Bob: 5 points Alice: 0 points |
Bob: 1 point Alice: 1 point |
|
| Numbers indicate points given (the more points the better). The overall maximum is achieved through cooperation (6 points) but the individual maximum (5 points) is achieved through defecting while the other player cooperates. In essence, points need only follow the relative ranking showed. | |||
If Bob is looking out for his own interests he will make the following analysis: if he suspects that Alice will cooperate then he should defect (he would get 5 points instead of 3) and if he suspects that Alice will defect then he should also defect (getting 1 point instead of 0). Alice makes a similar analysis and mutual defection ensues (1 point for each; a suboptimal outcome).
Often, of course, more than two players compete for the same resource. In the case of n-player games a mathematical approach may be impractical sometimes leading to the use of simulations or more prose-oriented approaches. One famous example often invoked within political science is Garrett Hardin's (1968) "Tragedy of the Commons." Hardin, discussing pollution of the environment, calls upon the analogy of a collectively owned pasture. Although the continued existence of the commons might constitute a collective good, each individual farmer is tempted to exploit (over-graze) it. Again we find a "social dilemma," individual rationality (exploit the commons) is opposed to collective rationality (keep common resource). More specifically, in a social dilemma "each individual always receives a higher payoff for defecting than for cooperating, but all are better off if all cooperate than if all defect" (Dawes and Messick, 2000, p. 111).
Sum Type
A key to understanding game dynamics is considering the payoff sum. The crucial question is whether the sum is fixed or variable. In the first case one player's loss is another's gain. A stand-alone game of chess where the loser pays the winner 10 dollars would qualify. In such a case there is no reason for negotiation since there is no sense in cooperating: Both players' self-interest dictates that they try to reduce the opponent's payoff. Such games are termed zero-sum, as the total sum of the players' gains and losses equals zero. Let's imagine, however, that our chess-players enter a tournament with the additional special rule that each opponent pawn killed earns the killing player 1 dollar, paid by the tournament sponsor. In this case the sum is not fixed; the game is non-zero sum (or variable sum), as the total sum of gains and losses experienced by the players is not necessarily zero. This calls for rather different strategies among the players and would inspire cooperation to a certain degree - for instance, by agreeing to perform a mutual sacrifice of all pawns before battling it out with the remaining pieces. The Prisoner's Dilemma is a non-zero sum game as the size of the combined pay-off depends on aggregate player choices.
Single-shot Games versus Repeated Games
The strategic dynamics may be quite different between games which are only played once (single-shot games) and games that are repeated. In single-shot games, players seek short-term gains while players of repeated games will be able to make short-term sacrifices in favour of perceived long-term opportunities. For instance, a single-shot Prisoner's Dilemma ends in mutual defection but a repeated version may not. The players in the repeated version operate under what Robert Axelrod (1984) has called "the shadow of the future": their actions in any given round will have consequences in later rounds. Thus, one very (if not universally) successful strategy is Tit-for-Tat, the prescription that one should start by cooperating and then do whatever the other player did in the previous round (Axelrod, 1984). By punishing defectors while not angering vengeful opponents, such as other versions of itself, Tit-for-Tat can manage to generate the trust necessary for collectively successful play (the cooperate-cooperate instance shown above). Often, the implication of interacting repeatedly with the same people will be that reputation becomes highly important.
Equilibrium
In a standard one-round version of the Prisoner's Dilemma, rational players will not cooperate. Thus, they get a payoff that could have been larger (if they had trusted each other) but are stuck in a situation where neither player by changing his strategy can do any better. The Prisoner's Dilemma, then, has an equilibrium (although a so-called deficient one since overall the players could do better); the game calls for particular strategies and players will not deviate from their set course. An equilibrium, then, may be thought of as a game state to which the game is likely to gravitate and once reached the players will generally not change their strategies. A game may have any number of equilibria including none and these may be either of the pure strategy type where players play one particular strategy or of the mixed strategy type where players randomly pick a strategy each round. An example of the latter is rock-paper-scissors where rational players need to play one of the three available strategies with the probability of 1/3.
Implications for Computer Game Studies
The following section begins with a brief review of how game theory has already informed game studies and game design. This is followed by a discussion on how game theory is relevant on two levels: The design level where game theory can be of assistance on the issue of game balance and may lend inspiration to the design of dramatic situation types and a community management level where online game managers often want to encourage certain types of behaviour within the gamespace.
Being a formalization of ideas concerning strategic thinking in situations of conflicting interests, we should not be surprised that game theory as outlined above has already lent inspiration and concepts to work on computer games. Indeed, concepts like zero-sumness (or non-zero-sumness) have been assimilated into even non-technical language to the extent that the speaker need not be aware of their origin.
Looking at group formation in MMORPGs, Elina M. V. Koivisto (2003) points out that in games such as Anarchy Online "the non-zero sum experience sharing seems to encourage players strongly to form teams" (p.8). In other words, the relationship in payoff between a play-alone strategy and a play-together strategy has been altered in favour of cooperative play (assuming that players are point-maximisers).
Also, designers Andrew Rollings and Dave Morris (2000) consider game theoretical terms useful for ensuring game balance and discuss the problem of dominant and dominated strategies; strategies that have no effective counter-strategies and strategies that are never effective respectively. They suggest that variations of the rock-paper-scissors principle (no strategy is inherently stronger than others) can be applied to ensure balance and mention informative examples of games that have succeeded or failed in this account. Rollings' and Morris' discussion, obviously, is a reference to the issue of equilibrium as described above.
Recently, Katie Salen and Eric Zimmerman (2003), in their ambitious examination of game ontology and design have described how the tools of game theory may provide a fruitful perspective on games and have echoed Rollings' and Morris' conclusion that this perspective is a systematic way to approach the issue of game balance.
Looking beyond balance issues (that do tend to associate themselves mostly with strategy games), designer Markus Friedl (2003) proposes that the Prisoner's Dilemma may serve as a guideline for the design of situations of non-violent conflict in multiplayer online games. He stresses that the tension embedded in such situations can create interesting choices and dramatic situations as players consider whether to trust one another in dangerous circumstances[1]. Friedl, then, is among the first to suggest that game theory games themselves, and not just the concepts and tools of the discipline, may lend inspiration to designers attempting to create or inspire dramatically compelling situations. This possibility will be further discussed below.
These examples illustrate that game theory as a perspective (if not as a coherent theory) permeates some thinking on game design. Although Friedl does take the discussion in new directions, and despite the both useful and lucid nature of these accounts, they seem tied to quite technical or literal applications of basic concepts.
Design Issues
Before discussing the game design possibilities deriving from game theory we must consider how a few of the key concepts map onto computer games.
First of all, the concept of strategy may be superficially appealing but in terms of computer games it is not immediately obvious which level of analysis it refers to. In the Prisoner's Dilemma the possibility space was clearly defined: each player could choose one of two available strategies. But considering a game like Counter-Strike (2000) we see that a player may have strategies operating on multiple levels. She may play cooperatively, making sure her actions are in accord with team interest and be highly aggressive (as opposed to defensive) and choose to always attack using a certain combination of evasive manoeuvres and rapid bursts of fire. All of these levels are often discussed in terms of "strategy" but it is only an approach operating on the minimal units of player choice, which in fact corresponds directly to the game theoretical concept. And it is not clear what such a minimal choice unit would be. Fortunately, we can justifiably consider combinations of choices on lower levels to be a strategy on a higher level, which is what is usually done when game designers discuss issues regarding dominant strategies. Game designers Andrew Rollings and Ernest Adams (2003) examine an issue with the real-time-strategy game Warcraft (1994) in which the Orc player was almost guaranteed to win when producing warlock units. Such a possibility does rob the game of some strategic potential. But framing one's analysis in the language of strategies one should be careful not to conflate all game genres. In its classical form, game theory applies most directly to strategy games. In games where the implementation of one's decisions is itself part of the challenge, such as most action games, dominant strategies will be less of a problem. Indeed, in many non-strategy games the very act of working out a "best strategy" may be deeply entertaining.
Another aspect of computer games, which needs to be addressed before game theoretical concepts can be applied, is the distinction between single player and multiplayer games. In a game theoretical perspective single player computer games fall in two groups. Firstly, games in which the game environment does not respond adaptively to the actions of the player are completely comparable to "games against nature." In an early arcade game like Moon Patrol (1982) for instance, the alien enemies follow pre-programmed patterns of movement and fire. The environment is non-adaptive and the player does not have to factor her own actions into the picture when trying to infer how the enemies move. The situation is quite different in Pac-Man (1980). The movement patterns (or "personalities" as they are often labelled) of the enemy ghosts are different for each ghost and quite complex (Mateas, 2003). But crucially they also react to the player's movement in the sense that some of them will give chase if the player gets too close. Thus, the successful player must respond to her own perceptions of how the ghosts will react to her actions. From the perspective of the player the latter situation is clearly strategic but it is also different from playing against a human opponent as the Pac-Man player can still in principle deduce the underlying algorithms governing the environment. More modern single-player games, of course, usually have more complex Artificial Intelligence (AI) and while still rule-governed the behaviour of enemies may be heuristic and the AI may even learn based on the results of trial-and-error. An analytical decision on whether to group such games with single player games or multiplayer games when discussing strategy must depend on the purpose and focus of the analysis. Clearly there are differences (both in terms of gameplay and player experience) between playing an advanced AI and playing another person but to a large extent the ways in which players strategize is likely to be comparable.
While acknowledging that certain game theoretical concepts do not map effortlessly onto computer games it does seem fair to assume that since game theory provides a systematic and clear vocabulary for discussing strategic behaviour an understanding of its basic concepts is likely to benefit designers of many game types. Also, for the game analyst or critic a vocabulary for discussing balance issues is likely to be advantageous.
What is likely to be applied here is not a mathematically rigorous analysis of payoffs, since games of even minor complexity will inspire real players to a variety of slightly varied mixed strategies, but rather an understanding of how strategies interact and a heightened attention to equilibrium situations. Regarding strategy games at least, such situations present the direct opposite of "interesting choices," Sid Meier's brief definition of good gameplay. If, in a strategy game, the strategy get to technology level three then send entire army against opponent is the best a player can do regardless of the other player's actions the game will lose its strategy element and rather become a game of hand-eye coordination. However, as the above discussion on strategy implies, the notion of strategic dominance and its implications for game design are not as straightforward as sometimes argued.
To illustrate how game theory may actually inspire the design of entirely new dramatic situations, consider the game of "Chicken." In this activity drivers race towards each other and the first to swerve loses the game. Obviously, if neither swerves, both get the worst possible outcome of the game. What is the best strategy? Again, this depends entirely on what you expect your opponent to do. Consider the following, however. Our thrill-seeking drivers, let's stay with Bob and Alice, are still racing towards each other processing levels of probability in their minds. Is there a way for Bob to get an edge? A highly powerful approach would be for him to limit his own options by tearing off the steering wheel and tossing it out the window for Alice to see. Effectively, he will (if all goes well) have changed Alice's payoff matrix to the effect that she now faces the choice between defeat (bad) and death (worse).
In line with "strategic ignorance," the purposeful avoiding of information, we can call this an act of 'strategic impotence'. A famous literary example, of course, would be Odysseus having himself tied to the mast to avoid being tempted by the song of the Sirens. For more modern day examples, consider leaving your credit card at home to avoid overspending, or having time delays on the opening of bank vault to avoid being forced into opening them by robbers.[2]
Now, can such a principle be employed in computer games?
Unless facing an expected loss of agency (say, the avatar turning into an all-slaying uncontrollable monster at certain intervals), merely limiting one's options in order to avoid temptation in a game is not likely to be useful. However, strategic impotence might provide worthwhile variation in many action or strategy games. Imagine a real-time-strategy game where Bob attacks Alice's camp. Under traditional circumstances, Alice will consider the strength of Bob's army judging by his previous performance in the game and other indicators to that effect. She will also wonder about Bob's commitment to the attack, wondering whether he is really just trying to scare her into leaving her settlement without a fight. However, consider the alternative situation where Bob commits a portion of his forces to an all-out attack (perhaps invoking a "berserk" feature that justifies his sudden lack of control). In this case Alice knows what she is facing but is also aware that no matter what she throws at Bob he won't back down. Thus, Alice will be weighing the value of her camp against the losses she is likely to suffer at Bob's hands. She might well consider a timely retreat while keeping in mind that she does not want to be known as someone who folds under pressure. Thus, including the option of strategic impotence in the form of commitment to all-out war (or indeed to an all-out aggressive response) may alter the game in entertaining ways. Also, commitment does not need to be technical. It can be quite social if, say, Alice on a widely used, highly visible game community board proclaims that she will throw all her powers against anyone who attacks her inside a multiplayer strategy game. A subsequent failure to do so will leave Alice bereft of her credibility and her ability to make similar threats in the future, thus creating the non-technical, peer-regulated equivalent of a contract. In this case the design challenge changes to one of carefully constructing a game-external "social" interface that allows such commitments to be constructed (and deviance from them to be regulated or punished).
Community Management
The design issues mentioned above centre on combining a level playing field with interesting opportunities for strategizing. Game balance, then, is about noble war and not about ensuring peace. However, in a broad range of game-related situations, peace, or at least constructive behaviour, is exactly what may be desired. To the surprise of early online game developers technical challenges have often been dwarfed by social issues (Morningstar & Farmer, 1991). In recent years, MMORPG players and developers have had to cope with phenomena such as cheating and grief play, the latter term being poorly defined but including activities such as player-killing, kill-stealing, monopolizing spaces or in-game trade ( Smith, 2002; Foo, 2004)[3]. Developers have been forced to take the issue quite seriously as is evident from the FAQ of Mythic's Dark Age of Camelot:
''An unfortunate situation has arisen in several currently-available online games where some game players go out of their way to ruin the gaming experience for other players by killing them repeatedly, "stealing" their monster kills, and generally making an[sic] nuisance of themselves. Camelot has several built-in methods for discouraging this behavior.'' http://www.darkageofcamelot.com/about/faq.php
Although the analogies deserve more attention than can be given here, it would seem clear that many types of crime, cheating and harassment in virtual worlds can be seen as problems of social order. On the issue of managing social tension, games such as MMORPGs do not as a group differ from explicitly social virtual worlds although clearly arguments as to what constitutes acceptable player behaviour may be less than clear-cut in games focusing on crime and violence.
Thus, work on conflict management and social dilemmas within other multi-user systems (e.g. Kollock & Smith, 1996; Donath, 1999; Smith, 1999) is nearly directly applicable to the design and study of game sociality.
Much of this work, in turn, builds on analyses that could well be called game theoretical. Through the history of political theory thinkers have struggled with the design of systems that would ensure the desired level of social order without sacrificing citizen freedom or happiness. For instance, in Leviathan political philosopher Thomas Hobbes (1651) framed the problem as one of selfish agents agreeing to instate a neutral third party (the sovereign) who would punish non-cooperators. The agents in question would do this because of their shared desire to undercut the deficient equilibrium of the Prisoner's Dilemma. With a more positive view of human nature, Adam Smith (1776) described how capitalist specialisation turned the market into a non-zero-sum-game thus in itself going a long way to increase the likelihood of cooperation. Thus, political theory supplies two general models for ensuring cooperative behaviour, a neutral-third-party approach and a structural-design approach that does not require constant (and costly) monitoring by a neutral guarantor. Since the first can be costly the latter is likely to be preferred by most game designers (although reputation systems and similar approaches have sparked much discussion, it appears that these insights have not been formally presented in relation to game design).
In order to reverse the analysis from one of finding rational strategies to one of inspiring cooperative behaviour through system design one has to make assumptions as to player rationality. And while one cannot predict the exact payoff matrices of individuals, by making life hard on grief players such behaviour is likely to be discouraged. By analogy, the existence of real-life police forces do not eliminate crime altogether (criminals have different payoff matrices than non-criminals) but few would claim that they do not diminish crime rates.
Now, if we assume a modicum of behavioural and preferential consistency a number of analyses shed light on the structural requirements for cooperative behaviour. Importantly, Robert Axelrod's seminal The Evolution of Co-operation has shaped much debate by formalising what he posits are three key requirements: the need for persistent identities, memory of past interactions, and repeated interaction[4].
Moving beyond the issue of unpredictable preferences, Elinor Ostrom (1990) has scrutinized actual successful communities to identify common features. One of these is clearly defined group boundaries. This rhymes well with Axelrod's emphasis on recognition and the necessary chance (or risk) of future interaction. It also rhymes well with old-time LambdaMOO users referring to early times as "a Golden Age - a time when MOOers lived in peace and productivity and had no need of rules or disciplinary structures..." (Dibbell, 1999, p. 96) and Julian Dibbell's (1999) description of how they bewailed the "declining quality of Lambda life and called for an immediate locking of the gates against the newbie hordes" (p. 204).
Thus, if once again we relax the requirements for exact mathematical modelling, game theory and related disciplines can yield powerful insights into the design and study of online worlds.
Case Study: Age of Kings
Having outlined the game theoretical perspective and suggested two areas where it might inform design and research, I will now apply the concepts to a concrete game, Microsoft's real-time-strategy title Age of Empires II - Age of Kings (with the Conquerors expansion; AOK hereafter). Whereas balance issues are of obvious interest in strategy games, I will also describe how AOK (or rather its online matching service) faces serious trust issues. Issues, then, that are not only relevant in the monster-ridden worlds of MMORPGs. The aim of this case study is not to perform a thorough analysis of the game but rather to highlight game aspects that lend themselves to a game theoretical analysis.
AOK at First Glance
AOK is a real-time-strategy game following most of the genre standards put in place by Virgin Entertainment's Dune II in 1993. The players struggle for domination of an area with natural features serving as obstacles or resources to be gathered. Typically the game map starts off unexplored and a "fog of war" hides changes in areas not in the line of sight of the player's units. Individual players must balance the variables of the game in the attempt to eliminate the opposition (or fulfil other optional criteria of success such as building a wonder). Since resources are scarce and speed is crucial there is a tension between armament and the development of one's nation, which goes through a series of ages, ranging from the Dark Age to the Imperial Age. As the nation advances through the ages, new units and upgrades become available leading to severe disadvantages for those who fall behind. Obviously - and this is what makes the game strategic - a sensible choice of strategy depends on one's perceptions of other players. Thus, if Alice's scout discovers nearby opponents concentrating their efforts on raising an army Alice will probably feel inspired to do the same. Having had a glimpse of the opponent's units she will probably want to create units that counter the enemy army well (in this case for instance pikemen against cavalry).
The strategic effort required is increased by the choice of civilizations such as Vikings, Babylonians or Teutons (common since Dune II and established as a de facto standard in strategy games since Sid Meier's Civilization) with individual technology trees, strengths and weaknesses. Adding to the complexity, team play introduces bonuses for certain combinations of civilizations.
Game Types and Strategic Consequences
In this section I will focus on the consequences of certain game settings as well as more traditional issues showcasing how game theory can be (and often is) used to address questions of game balance.
Having braved the player matching of AOK, players are in fact not yet ready to play. Another set-up screen must be traversed. Here teams (if any) are formed and civilizations chosen. Settings not chosen before may be negotiated and finalized at this stage. All settings impact on other choices (e.g. choice of water map increases the relative strength of seafaring civilizations). However, one setting type relates directly to the game types discussed above: the victory conditions. Now, in rated games the scoring system is technically zero-sum. One side gains what the other side loses although with the special principle that the number of redistributed points depends on the difference between player ratings (beating a player of much higher rating triggers a huge score). Consequently, there is not an obvious motivation for cooperating or negotiating with the other side within the game (although communication may of course serve as bluff, taunts etc.). However, the availability of certain game types changes the situation.
The most important game types for our purposes are: Conquest, Regicide, Wonder, and Last man standing. Of these, Conquest is the free-for-all battle where one player (or team) wins by eliminating the others. In a Regicide game the death of a certain unit means defeat (much like chess) and in Wonder the first player to build and subsequently defend a wonder wins. In Last man standing the team, which eliminates the others, is dissolved leading to a final battle between former teammates.
Likely strategies will depend on the choice of victory conditions. This is not to say that game type determines strategy. It obviously doesn't since certain knowledge of other players' strategies would make a player (indeed all the players) choose a different one in the absence of actual dominant strategies. But it does mean that the game type inspires (or affords) certain strategies. In Regicide or Wonder, for instance, getting rid of the opposition is obviously an advantage but less than crucial for achieving the objective. Thus, if a player is planning to build a wonder and defend it he or she is likely to prioritize defence highly, leading to the construction of guard towers and heavy walls. These game types also inspire sudden alliances since one player constructing a wonder will immediately mean a certain convergence of interests of all other players. In order not to lose, everyone will need to attack the wonder before the builder wins. Such a situation is in fact a Prisoner's Dilemma variation. While all members of the alliance-of-necessity need the threatening wonder eliminated it would be best for any individual alliance member if the others were to bear the cost leaving the martyrs weak once the wonder falls. However, if noone takes on the wonder the whole alliance loses.
Stepping away from player strategies and onto the battlefield, AOK units are carefully balanced to avoid obvious and uninteresting choices, in other words to avoid equilibria. The model used is typical of strategy games and can be though of as deriving from Rock-paper-scissors (see above). In the case of AOK (discounting upgrades) the relationship between basic units can be illustrated as follows.
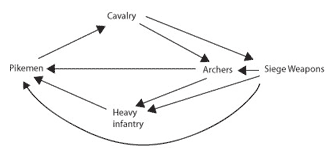 Relationship between major units in AOK
Arrows indicate special countering capacity (i.e. pikemen counter cavalry etc.)
Relationship between major units in AOK
Arrows indicate special countering capacity (i.e. pikemen counter cavalry etc.)
Consequently, no single unit is useful in all circumstances, although the distribution of units in a given game is rarely equal due to production costs, etcetera. For instance most games will feature more infantry units than siege units.
Game theory, then, provides a framework for discussing such dynamics and both practical and conceptual tools for understanding/avoiding unpleasant game dynamics and for predicting player behaviour to some degree.
Trust and Unknown Opponents
The discussion below will centre on issues that might not traditionally be considered directly game-related although I hope to show that they are crucial to the actual game experience.
For online play AOK players go to Microsoft's gaming system Zone.com, a site hosting both free online games and commercial, boxed titles.
Within this system players choose between a variety of game "rooms" of various types (e.g. tournament play, rated, non-rated, etc.). Once inside a room a specific game is chosen (or created). This brings the player to a chat screen and to a description of the settings chosen by the game host.
The following is an example of such a pre-game chat-session:
(Enter) > takeshi128
takeshi108> hi
(Enter) > vBerlichingen
BIL_him> hi
vBerlinchingen> hi
Lord_Wumpus> hi all
(Enter) > bobbob321
bobbob321> is there rushing?
[Pause]
(Enter) > lillosub
lillosub> hi all
takeshi108> it means that there perhaps rushing
(Exit) > takeshi108
Odlakarab> yes
This brief snippet exemplifies a (admittedly superficial) negotiation of rules. Rushing is the common term for early attacks within the game, attacks that if successful may well cripple the victim and end the game quite quickly (relative to the 60-90 minute norm which depends on number of players, map type, etc.). While the game has numerous settings, it is not possible for the players to actually eliminate the option of rushing on a technical level. Bobbob321, immediately upon entering, wants to know of rushing is allowed, practically asking for a promise that may or may not be kept once the game starts. A period of silence follows his question and takeshi108 takes this to mean that bobbob321 shouldn't feel secure ("it means that there perhaps rushing"). Odlakarab agrees ("yes").
What are the ways for players like bobbob321 to judge the situation and the trustworthiness of potential opponents? This could also be framed as a question of whether the AOK matching system has any trust issues.
Now, a player entering the system is provided with some information about his opponents. First of all, he or she is provided with their rating, a number starting at 1600 and rarely moving below 1000 or above 2000. It isn't, however, necessarily the case that a high rating corresponds to a skilled player. In a concrete case there may be many reasons for such a discrepancy but on a general level an important way to lose rating is to disconnect from a large number of ongoing games. Obviously, such behaviour may be attributed to unstable connections, personal issues, etc. but since it can obviously be used for strategic purposes (to avoid near-certain defeat) it cannot be allowed to go unpunished. However, the number of times a player has disconnected is also evident from his or her profile. Importantly, a player's ping (latency) is also displayed and its quality is directly related to the extent that one is welcome in a game (the higher the better, of course, since low pings may slow down the game for everyone). Thus, veterans (and indeed anyone willing to study the intricacies of the way score is calculated) can easily extract large amounts of information from the numbers. Rating and number of disconnects are trustworthy signals to the extent that they are tied to the player who has been responsible for the profile. In this sense they are not strategically important, they cannot directly be hidden, faked or used to bluff.
However, even with standard game settings at least three elements go directly to the issue of trust. The first is commitment to the game or the ability to fulfil one's commitment. Unless your opponent has a high rating and very few disconnects you could speculate that that player might not be relied upon to complete an actual game (thus creating an unpleasant experience for all involved, perhaps forcing everyone back to the player-matching system). One indicator that might make someone worry about another's ability to actually realize a desire to play is poor spelling. This could well indicate low age which is, again, an indicator of low autonomy. Despite the player's claims to the contrary, a child's parents might suddenly decide that it is time for bed and turn of the computer. Alarm bells might also start chiming if someone reacts very slowly or doesn't chat at all. Low commitment to the interaction might indicate that the player plays under distracting circumstances that might cause him or her to disconnect or to be a highly unfortunate ally in the case of team games.
The second danger to worry about is secret alliances. This is obviously only dangerous in free-for-all games or team games where players can switch between teams. For games with permanent teams there would (typically) be no sense in pre-game scheming.
Imagine two players arriving at the game-chat for a free-for-all game at roughly the same time perhaps with identical sounding names (e.g. Scandinavian sounding). They may claim to be strangers but one cannot really know if they have arranged to kill off everyone else and finish the game in a way that secures points for both of them.
The third danger is one of incorrect ratings. Whereas one cannot fake the rating of a given profile there are several reasons why the player may actually be much more skilful than the ratings imply. First of all, the player may be so veteran that his real rating scares off anyone within the system leaving him with no opponents. In order to play at all (and perhaps have some fun with naive newbies) he could create a new profile and appear with a 1600 rating. Thus, the newbie rating would actually be taken as a sign of potential danger and indeed master players posing as newbies have been feared within the game giving rise to the term "smurfs." Distrust towards newcomers is an unfortunate consequence of having any degree of persistent identities, which, as mentioned above, is in itself an essential feature for ensuring trust in many interactions[5]. Now, having scrutinized the game matching situation under the assumption of high risk-adversity can we expect players to actually display this degree of paranoia? Yes and no. Obviously, gamers may be expected to care. A single game, depending on settings, may well last more than an hour (single games have been known to last more than five times that). Consequently having one player disconnect halfway through is quite frustrating even if the person is an adversary since the game will then be over or may become seriously imbalanced. Much playing time will have been lost. In rated games where players complement their desire for fun with a desire to actually improve their score, disconnects (on the opposing side) may be less frustrating. However, such players may be expected to place increased importance on the danger of secret alliances and incorrect opponent ratings. On the other hand, an obvious concern will deter all but the most rating-conscious player from tirelessly attempting to achieve absolute certainty as to the opponent trustworthiness: time. In economic terms, prolonged scrutiny inflicts an opportunity cost on the player: Time spent wondering about safety issues is time not spent playing. Thus, actual player behaviour may be said to mirror the player's perceived cost of time spent on pre-game chatting as opposed to play time. Since careful analysis comes at a price (measured in time and perhaps money in the case of non-flatrate dial-ups, etc.), the game theoretical perspective can encompass players who throw caution to the wind and attempt to start games as fast as possible. That would be a perfectly sensible strategy for someone who perceives in-game risks to be slight and chat to be a severe waste of time.
If we were to assume that players come to actually play and also in fact have a tendency to prefer victory over defeat we might expect the trust issues outlined above to have certain consequences for the AOK matching process. One would be that games (and particularly "rated" games, which count towards the player's rating in the system) would have a hard time actually being started[6]. These issues might also explain why the developers in the follow-up title Age of Mythology (2002) chose to eliminate all need for pre-game communication and base the matching exclusively on clearly defined rules[7].
Summary and Perspectives
This article has argued that economic game theory, while neither focusing on recreational games nor being concerned with fun in any way, can provide tools for understanding and designing computer games. Having described game theoretical concepts that may add to a systematic vocabulary of game analysis the article has argued that such an approach can most directly inspire work on design (and analysis) particularly on the topic of game balance and on the issue of community management. The latter being central to online worlds such as MMORPGs and to those matching and tournament interfaces that face problems of trust. Through a case study of a real-time strategy game the article illustrated how a game theoretical perspective might add to the understanding of game dynamics.
Notably, the game issues not covered by a game theoretical perspective are, obviously, legion. It is not a grand theory that can replace or encompass others but rather an important toolset for the analyst of strategy and social dynamics of multiplayer games.
The elements addressed in this article have been mostly theoretical in the service of providing a foundation for further work. This work could well entail empirical analyses of player behaviour patterns or take the form of actual experiments with the relation between behaviour and settings highlighted by the theory.
More concretely, if one wishes to discourage some form of grief play it would be worthwhile, indeed quite obvious, to attempt an analysis of grief player motivation. Qualitative methodologies could thus provide crucial data on grief player preferences, which could aid designers in influencing the behaviour of the players in question.
Regarding grief play, a thorough "typology of grief" might also yield important insights. The risk of grouping all undesired behaviour into one is blindness to the likelihood that some behaviour should be approached with tools from system security, some with tools from political science, social psychology etc. Thus, such an effort would also help make clear to what extent games and virtual worlds can be said to entail public goods and consequently how well the theories of such goods are appropriate for the study of player behaviour.
Furthermore, it would be enlightening to apply insights from the field of experimental economics, which tries to test actual human behaviour in clearly defined situations of conflicting interests, to issues of player behaviour and "type." In all likelihood, the player types evident in work on value orientations could be fruitfully combined with computer game player typologies such as Richard's Bartle's taxonomy of MUD players (Bartle, 2003).
Clearly, such approaches would capitalize on work already done, inspire new directions for game research and showcase the links between game studies and other disciplines.
The author is grateful to Edward Castronova and Thomas Wedell-Wedellsborg for feedback on earlier versions of this article.
References
Axelrod, Robert. (1984). The Evolution of Co-Operation. London: Penguin Books.
Bartle, Richard. (1996). Hearts, Clubs, Diamonds, Spades: Players Who Suit Muds. Website. Retrieved November 27, 2003, http://www.mud.co.uk/richard/hcds.htm
Battle.net. (2003 September 30). Starcraft, Diablo Ii, and Warcraft Iii Accounts Closed. Website. Battle.net. Retrieved November 14, 2003, http://www.battle.net/news/0309.shtml
Camerer, Colin F. (2003). Behavioral Game Theory: Experiments in Strategic Interaction. Princeton: Princeton University Press.
Dawes, Robyn M., and David M. Messick. (2000). "Social Dilemmas." International Journal of Psychology 35, 2, 111-16.
Dibbell, Julian. (1999). My Tiny Life. London: Fourth Estate.
Donath, Judith S. (1999). "Identity and Deception in the Virtual Community." Communities in Cyberspace. Ed. Peter & Smith Kollock, Marc. New York: Routledge.
dustin_c1. (2003 October 13). Esonline - First Look. Website. MrFixitOnline. Retrieved November 27, 2003. http://www.mrfixitonline.com/aom-esopreview.asp.
Foo, Chek Yang. (2004). "Redefining Grief Play." Other Players - a conference on multiplayer phenomena. Eds. Jonas Heide Smith and Miguel Sicart. Copenhagen.
Frank, Robert H. (1988). Passions within Reason - the Strategic Role of the Emotions. New York: W. W. Norton & Company.
Friedl, Markus. (2003). Online Game Interactivity Theory. Hingham: Charles River Media, Inc.
Hardin, Garrett. (1968). "The Tragedy of the Commons." Science 162, 1243-48.
Hobbes, Thomas. (1651/ 1997). Leviathan - or the Matter, Forme and Power of a Commonwealth Ecclesiasticall and Civil. New York: Touchstone.
Juul, Jesper. (2003). "The Repeatedly Lost Art of Studying Games - Review of Elliott M. Avedon & Brian Sutton-Smith (Ed.): The Study of Games." Game Studies 1, 1.
Koivisto, Elina M. I. (2003). "Supporting Communities in Massively Multiplayer Online Role-Playing Games by Game Design." Level Up - Digital Games Research Conference. Eds. Marinka Copier and Joost Raessens. Utrecht: Utrecht University.
Kollock, Peter (1998). "Social Dilemmas: The Anatomy of Cooperation." Annual Review of Sociology. 24,183-214.
Kollock, Peter, and Marc Smith. (1996). "Managing the Virtual Commons - Cooperation and Conflict in Computer Communities." Computer-Mediated Communication: Linguistic, Social, and Crosscultural Perspectives. Ed. Susan C. Herring. Amsterdam: John Benjamin.
Mateas, Michael. (2003). "Expressive Ai:Games and Artificial Intelligence." Level Up - Digital Games Research Conference 2003. Eds. Marinka Copier and Joost Raessens. Utrecht: Utrecht University Press.
Morningstar, Chip, and F. Randall Farmer. (2003). "The Lessons of Lucasfilm's Habitat." The New Media Reader. 1991. Eds. Noah Wardrip-Fruin and Nick Montfort. Cambridge: The MIT Press.
Neumann, John von, and Oskar Morgenstern. (1944/ 1953). Theory of Games and Economic Behaviour. Princeton: Princeton University Press.
Ostrom, Elinor. (1990). Governing the Commons - the Evolution of Institutions for Collective Action. New York: Cambridge University Press.
Poundstone, William. (1992). Prisoner's Dilemma. New York: Anchor Books.
Rollings, Andrew, and Ernest Adams. (2003). Andrew Rollings and Ernest Adams on Game Design. Boston: New Riders Publishing.
Rollings, Andrew, and Dave Morris. (2000). Game Architecture and Design. Scottsdale: Coriolis.
Salen, Katie, and Eric Zimmerman. (2003). Rules of Play - Game Design Fundamentals. London: The MIT Press, 2003.
Smith, Adam. (1993). An Enquiry into the Nature and Causes of the Wealth of Nations. 1776. Oxford: Oxford University Press.
Smith, Anna DuVal. (1999). "Problems of Conflict Management in Virtual Communities." Communities in Cyberspace. Eds. Marc A. Smith and Peter Kollock. London: Routledge.
Smith, Jonas Heide. (2002). "The Architectures of Trust - Supporting Cooperation in the Computer-Supported Community." MA Thesis. University of Copenhagen.
Smith, Jonas Heide. (2003 September 11). Avatars You Can Trust - a Survey on the Issue of Trust and Communication in Mmorpgs. Retrived November 10, 2003, http://www.game-research.com/art_avatars_trust.asp.
Smith, Jonas Heide. (2004)."Playing Dirty - Understanding Conflicts in Multiplayer Games." 5th annual conference of The Association of Internet Researchers. The University of Sussex.
Ward, Mark. (2003 September 29). Does Virtual Crime Need Real Justice? Retrieved November 11, 2003, http://news.bbc.co.uk/1/hi/technology/3138456.stm.